dimensions

From my last blog, the number of dimensions quantifies the information to navigate a space. Doodling away on a piece of paper, we need two numbers to find any speck on this paper. Most familiar is the 3-dimensional space around us. But we have already seen that 4-dimensional spacetime has its merits to navigate this universe.

How do we understand a high dimensional space?

Our brain is particularly adapted to navigate 2 and 3-dimensional spaces: we might need a map to walk from the Institute of Contemporary Arts to the National Gallery in London, but the 3rd dimension - the height of the buildings - does not play a role in this: we navigate a 2-dimensional space: the surface of the Earth.

The heights of shelves and desks, on the other hand, are relevant for, e.g., furnishing our living room. The familiarity lets us believe that we understand 2 and 3-dimensional spaces. Our brain is exceptionally bad to visualise, say, a 4 or 5-dimensional space. Do those spaces exist? - They do: spacetime is one obvious example for a 4-dimensional space. String Theory might finally be the theory that establishes the connection between quantum physics and gravity. To avoid that String Theory contradicts itself, it is a theory that lives in 10 dimensions. True - we only observe 4 around us (space & time). This means that String Theory also has to explain how 6 of the 10 dimensions are curled up and only visible in extremely high energy experiments.

Encounters with high dimensions are rare, and evolution has not given our brains a chance to internalise the concept. What should we do?

In this blog, I will illustrate how Mathematics can help us to get a grip on n-dimensional spaces. To this aim, we will distil the essence of being a cube into a Mathematical framework. We will then use the framework to build cubes in other dimensions than 3.

As a side remark, Einstein raised a fundamental question: why is Mathematics describing the universe so well? This is the scary bit: whenever Mathematicians build a new concept, it is somehow at work in nature. What use is a space where you can have two distinct points with zero distance, yet it is not the same point? Answer: it is the world around us - spacetime.

What’s a cube?

Let’s get started and look at a cube. Since from now on it is all Mathematics, it is helpful to be precise: If you look at the adjacent figure, you don’t see a cube. You see a cube projection on the 2-dimensional screen of your mobile, tablet or PC.

What’s a projection? Assume you look at the above wireframe through your living room window. Put a sheet of semi-transparent paper on your window, and copy the edges of the wireframe onto the sheet. You get what you see now on your screen. Why is this hard to notice? The categorisation is an evolutionary advantage of our brain: it maps what we see to categories such as food, danger, friend or foe. We can hardly resist our brain screaming that our projection is that of a cube in 3 dimensions.

Mathematicians! They like to split the hair in the middle. Perhaps. Since it is our only tool to understand a 4-dimensional cube later, I just mentioned projection now.

I am not insisting.

Giving our brains the peace and quiet to interpret the projection as a 3-dimensional object, we would use 3 coordinate axes (x,y,z) to handle what a cube is.

What is, mathematically speaking, the essence of “cubism” (not to be confused with the art direction invented in 1907)? We will move (walk or fly) through space and trace out the wireframe until the cube is complete. These are the rules for the moves:

• Pick an axis and move a given length L in this direction.

• Once you traced out the distance L, pick one of the other directions to move next.

• Do not choose the axis you were coming from (e.g., if you moved along the x-axis, you only can pick y or z next).

• If you already moved along this axis before, you now move in the other direction (e.g., if you moved along the x-axis from left to right before, you need to move next time from right to left).

• If you have a choice at a vertex, choose the direction in the positive axis direction (but obey, at all times, the rule above).

• If you reach a vertex where you have been before, choose any other vertex with a direction not yet visited.

• If there is no more direction to explore, i.e., if each vertex has precisely n connections, you teased out the entire cube in n-dimensional space.

These rules seem elaborate for defining a cube. They have the unique advantage that we don’t specify the number of dimensions at any stage. Hence, these rules produce a cube in 3-dimensions (as we will check below) and let us construct a cube for any other dimensions.

Mathematically, the hard part is to convince yourself that the above rules cannot produce a set of lateral faces, hanging around and not forming the faces of the cube.

Let’s check that the rules work for a 2-dimensional space.

We pick the x-axis and the direction “left-to-right” for the first stage. We thus move from (A) to (B). At (B), we need to pick another direction. There is only the y-direction. We have two choices to move: up or down (both work). In the adjacent picture, I have chosen “up” and proceeded to (C).

At (C), we are coming in along the y-direction. Hence, the only other axis is the x-direction. Now, we don’t have a choice for the direction: we moved before from “left-to-right” (positive axis direction). We now must move from ”right-to-left”. We arrive at (D). No choice for the axis: it has to be the y-axis, and no option for the direction: before we moved “up”, now we need to move “down”. We are back at point(A), and there are no more directions to explore: each vertex has 2 wired ends. A “cube” in 2 dimensions is a square!

Finally, let us study the case of 3 dimensions.

Constructing a 3-dimensional cube.

The walkthrough space is indicated in the picture above. The first trajectory is in red. The steps are numbered from 1 to 12. Different colours describe different trajectories. There is a choice on which trajectory to embark next. Hence, don’t be surprised if you produce a cube with a different colour on the edges. You should, however, end up with a cube in any case.

Let us do some checks. We are supposed to visit the axes in alternating order. For the x-axis, we have the steps (1 4 7 9) and the directions are (+ - + -). For the y-axis, the visiting steps are (3 6 11 12), and the order of directions is (+ - + -). Finally, the steps for the z-axis are (2 5 8 10) and directions (+ - + -). Also note that each vertex has 3 wire pieces attached. We are done.

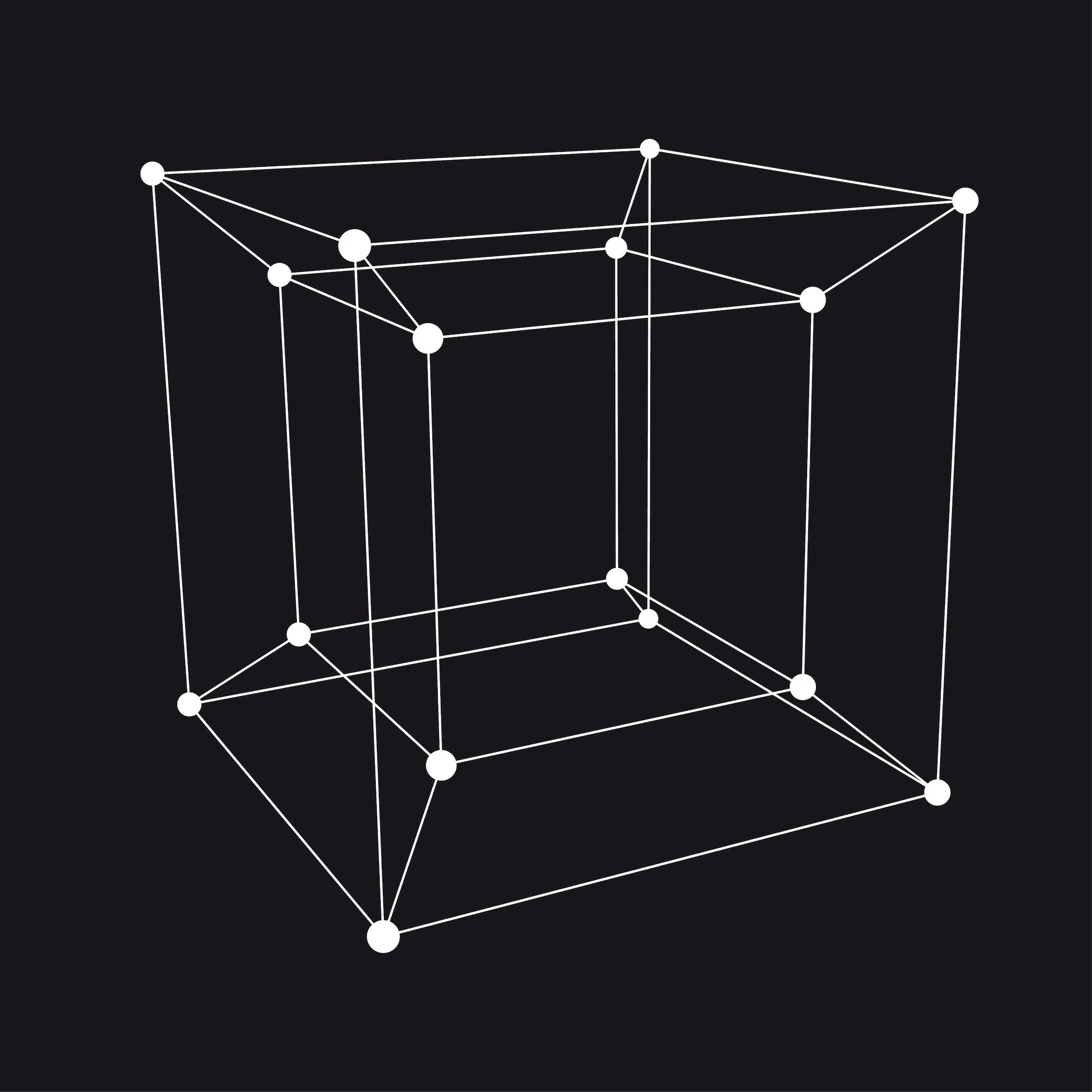
Tesseract

…is not a mountain region on an alien planet, although it sounds like it; it is a 4-dimensional cube. It’s depicted in the adjacent picture (or a projection of the Tesseract into a 2-dimensional flat screen, to be precise). Note that each vertex has indeed 4 wire pieces attached.

It is not entirely intuitive. It looks like a small cube inside a large cube with wires attached.

Your brain can help you to understand the 4-dimensional cube since your brain has experience with 4 dimensions, namely with spacetime. So, take the 4th dimension as time rather than another “spatial” dimension. In this case, we are always looking at a 3-dimensional familiar space and with time passing simultaneously. With this embedding, the Tesseract would indeed start out as a small cube at time zero and would then smoothly expand into the big cube at time L (the cube side length).

Does anyone dare to draw a 5-dimensional cube?